Conceitos básicos sobre Fator de Potência

Publicado em por

Nos circuitos CA, o fator de potência é a razão entre a potência real usada para realizar o trabalho e a potência aparente que é fornecida ao circuito. O mesmo pode obter valores no intervalo de 0 a 1.

Quando toda a potência é reativa, sem potência real (geralmente carga indutiva) – o fator de potência é 0.

Quando toda a potência é energia real sem potência reativa (carga resistiva) – o fator de potência é 1.

 

Definição de Fator de Potência

O fator de potência é igual à potência real ou real P em watts (W) dividido pela potência aparente | S | em volt-ampere (VA):

$ PF=\frac{P_{(W)}}{|S_{(VA)}|} $

PF – fator de potência.

P – potência real em watts (W).

| S | – potência aparente – a magnitude da potência complexa em voltagens (VA).

Figura 1- Triângulo de Potências

 

Cálculo do PF

Para corrente sinusuidal, o fator de potência PF é igual ao valor absoluto do cosseno do ângulo de fase de potência aparente φ (que também é o ângulo de fase de impedância):

$PF=cos\varphi$

φ   é o ângulo da fase de potência de aprendizado.

A potência real P em watts (W) é igual à potência aparente | S | em volt-ampere (VA) vezes o fator de potência PF:

$P_{(W)}= |S_{(VA)}|*PF = |S_{(VA)}| * |cos\varphi| $

Quando o circuito tem uma carga de impedância resistiva, a potência real P é igual à potência aparente | S | e o fator de potência PF é igual a 1:

$ PF_{(Carga Resistiva)} = \frac{P}{S} = 1 $

A potência reativa Q em volt-amps reativa (VAR) é igual à potência aparente | S | em volt-ampere (VA) vezes o seno do ângulo de fase φ :

$Q_{(VAR)} = |S_{(VA)}|* |sen\varphi |$

Cálculo do circuito monofásico a partir da leitura real do medidor de potência P em quilowatts (kW), tensão V em volts (V) e corrente I em ampères (A):

$PF = |cos\varphi| = \frac{1000 * P_{(kW)}}{V_{(V)}*I_{(A)}}$

Cálculo do circuito trifásico a partir da leitura real do medidor de potência P em quilowatts (kW), tensão linha a linha V L-L em volts (V) e corrente I em ampères (A):

$PF = |cos\varphi| = \frac{1000 * P_{(kW)}}{\sqrt{3}*V_{L-L(V)}*I_{(A)}}$

Cálculo do circuito trifásico a partir da leitura real do medidor de potência P em quilowatts (kW), linha a linha neutra V L-N em volts (V) e corrente I em ampères (A):

$PF = |cos\varphi| = \frac{1000 * P_{(kW)}}{3*V_{L-N(V)}*I_{(A)}}$

 

Correção do fator de potência

A correção é um ajuste do circuito elétrico a fim de aproximar o fator de potência de 1.

O fator de potência próximo de 1 reduzirá a potência reativa no circuito e a maior parte da energia no circuito será de potência real. Isso também reduzirá as perdas nas linhas de energia.

A correção do fator de potência geralmente é feita pela adição de capacitores ao circuito de carga, quando o circuito possui componentes indutivos, como um motor elétrico.

 

Cálculo da correção

A potência aparente | S | em volt-amps (VA) é igual à tensão V em volts (V) vezes a corrente I em ampères (A):

$|S_{(VA)}| = V_{(V)}*I_{(A)}$

A potência reativa Q em volt-amps reativa (VAR) é igual à raiz quadrada do quadrado da potência aparente | S | em volt-ampere (VA) menos o quadrado da potência real P em watts (W) (teorema de Pitágoras):

$Q_{(VAR)} = \sqrt{(|S_{(VA)}|^2-P_{(W)^2})}$

A potência reativa Q em volt-amperes reativas (VAR) é igual ao quadrado de voltagem V em volts (V) dividido pela reatância Xc:

$Q_{(VAR)} = \frac{V_{(V)}^2}{X_{C(\Omega )}} = \frac{V_{(V)}^2}{(\frac{1}{2*\pi *f_{(Hz)}*C_{(F)}})} = 2*\pi *f_{(Hz)}*C_{(F)}*V_{(V)}^2$

Portanto, o capacitor de correção do fator de potência em Farad (F) que deve ser adicionado ao circuito em paralelo é igual à potência reativa Q em volt-amperes reativos (VAR) dividido por 2π vezes a freqüência f em Hertz (Hz) vezes o quadrado tensão V em volts (V):

$C_{(F)} = \frac{Q_{(VAR)}}{(2*\pi*f_{(Hz)}*V_{(V)}^2)}$

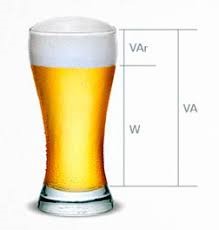
Potências aparente, reativa e ativa - Analogia Chopp

Figura 2 – Analogia Chopp – Potências Aparente, Ativa e Reativa

Fonte: EA – Engenheiros Associados